Noções Básicas de Conjunto

Representação de um conjunto

Os conjuntos são representados por letras maiúsculas e os elementos representados entre chaves por letras minúsculas.

Exemplos:

– O conjunto das letras do nosso alfabeto; L= {a, b, c, d,…, z}.

– O conjunto dos dias da semana; S= {segunda, terça,… domingo}  

– A representação de conjuntos pode ser feita de três maneiras:

1 – Por extensão:

Quando o número de elementos são finitos pequeno  suficiente para representá-los explicitamente.

Exemplos:

– Conjunto dos meses do ano; A = {Janeiro, Fevereiro, Março, Abril,…, Novembro, Dezembro}

– Conjunto das vogais; V = {a, e, i, o, u}

– Conjunto dos números pares positivos; P = {2, 4, 6, 8, 10, 12,…}

 2 – Por compreensão:

Um conjunto é representado por compreensão quando: é enunciada uma propriedade característica dos seus elementos. Isto é, uma propriedade que os seus e só os seus elementos possuam.

Exemplos:

B = {meses do ano}

D =  {os meus CDs de música}

P = {p ∊ N: p = 2q para algum q ∊ N}

Q= {x ∊ N: x é primo}

R = {x: x é um número natural par e positivo}

S = {x ∊ Z: 2≤x<5}

 3 – Por Diagrama

Consiste em representar os elementos de um conjunto internamente a um retângulo (geralmente) e os elementos dos subconjuntos, limitados por uma linha fechada e não entrelaçada.

Exemplo:

A é o conjunto das vogais do nosso alfabeto

Conjunto unitário

É o conjunto que possui um único elemento.

Exemplo:

A= { fevereiro},

B =  { número primo que é par}.

Conjunto vazio

É o conjunto que não possui elementos. É representado por: { } ou Ø.

Exemplo:

Assim teríamos: A= { } ou A = Ø

 Relação de pertinência

 Quando um elemento está em um conjunto, dizemos que ele pertence a esse conjunto.

Exemplos:
F = {0, 2, 4, 6, 8,…}
2  ∈  F →  lê-se: 2 pertence a F.
3  ∉  F→ lê-se: 3 não pertence a F.

Relação de Inclusão

Usamos os símbolos de inclusão de conjunto na relação entre dois conjuntos.

⊂  →  está contido             ⊄  →  não está contido        ⊃  →  contém         ⊅  →  não contém       ⊆   →  está contido ou é subconjunto ou é uma parte            A ⊆ B ⇔ ∀x(x ∈ A → x ∈ B)

Exemplos:

1)  Dados os conjuntos abaixo, E = {-2, -1, 0}, F = {0, 2, 4, 6, 8, …} e  G = {0, 1, 2, 3, 4, 5, 6, 7, …}. Podemos afirmar que F ⊂  G, G ⊃ F, E ⊅ F, F ⊄ E

2) A ⊂ B ou B ⊃ A

Subconjuntos 

Se cada elemento de um conjunto A pertence a um outro conjunto B, dizemos que A é subconjunto de B. Assim: A ⊂ B, que se lê: A está contido em B. Simbolicamente escrevemos:   A ⊂ B ⇔ (∀x) (x ∈ A ⇒ x ∈ B)

O conjunto A = {2, 3, 4, 5} é um subconjunto de  B = {1, 2, 3, 4, 5, 6} , pois cada um dos elementos de A se acha em B (note que a recíproca não é verdadeira). Quando dois conjuntos C e D têm todos os elementos em comum (C = D), implica em: C ⊂ D e D ⊂ C. Por exemplo o conjunto C ={3, 6, 9}  está contido em D = {9, 3, 6} e vice-versa.

Caso exista pelo menos um elemento de A que não pertença a B, dizemos que A não está contido em B, ou que A não é subconjunto de B.  Simbolicamente escrevemos:   ∃x /  (x ∈ A e x ∉  B) ⇒ A ⊄ B

Conjunto das Partes

Em geral, para qualquer conjunto A, pode-se construir um novo conjunto, cujos elementos sejam todos os subconjuntos possíveis de A. A esse novo conjunto chamamos de: Conjunto das partes de A, que é representado por P (A).    

 P(A) = {x/x ⊂ A}

Exemplo:

Sendo o conjunto A={2, 3, 5}, podemos escrever seus subconjuntos como segue:

Com zero elemento – { }

Com um elemento – {2}, {3}, {5}
Com dois elementos – {2,3}, {2, 5}, {3, 5}
Com três elementos – {2,3, 5}

Assim, temos:P(A) = { {  }, {2}, {3}, {5}, {2,3}, {2, 5}, {3, 5}, {2,3, 5} }

Pode-se demonstrar que, se n(P(A)) = k então, o número de elementos que formam o conjunto das partes de A, é dado por (P(A))=2^k.

Operações com conjuntos

 1 – União

A união entre dois conjuntos A e B consiste num outro conjunto C de todos os elementos que pertencem a A ou a B ou a ambos. Simbolicamente, temos: C = A ∪ B, lê-se: C é igual a A união B. De uma maneira mais concisa a definição dada acima pode ser escrita simbolicamente por:  A ∪ B = {x/x ∈ A ou x ∈ B}

Exemplo:

Fazendo a união dos conjuntos A = {2, 4, 7}  e, B = {1, 3, 4},  temos: A ∪ B = {1, 2, 3, 4, 7}  Também podemos representar a união usando diagramas:

2 – Intersecção

Chamamos de intersecção de um conjunto A com outro conjunto B, ao conjunto constituído pelos elementos x que pertencem tanto a A como a B, simultaneamente. A esse conjunto indicamos: A ∩ B, lê-se: “A intersecção B“, ou por simplicidade “A inter B“. Esquematicamente temos: A ∩ B = {x/x ∈ A e x ∈ B}

Exemplo:

Sejam L = {c, a, r, l, o, s}  e  V = {a, e, i, o, u}, temos: L ∩  V = {a, o} . Em diagramas:

3 – Diferença

Denominamos diferença A – B (lê-se: A menos B), o conjunto formado pelos elementos pertencentes a A e não a B, seja: Sejam L = {c, a, r, l, o, s}  e  V = {a, e, i, o, u}, temos:, temos que a diferença L – V = {c, r, l,  s} .

Em diagramas: A – B = {x/x ∈ A e x ∉ B}

4 – Número de elementos da união de dois conjuntos

Consideremos dois conjuntos A e B, iremos determinar os elementos de A por n(A), os elementos de B por n(B), a união de A com B por n(A U B) e a intersecção de A com B por n(A ∩ B).  A relação utilizando o diagrama:

n(A U B) = n(A) + n(B) – n(A ∩B)

5- Número de elementos da união de três conjuntos

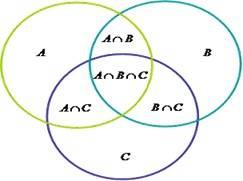
Considerando os conjuntos A, B e C teremos a seguinte relação na determinação do número de elementos:

n(A U B U C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A U B U C)

Exemplo
Uma avaliação contendo duas questões foi dada a 200 alunos. Sabendo que:

– 50 alunos acertaram as duas questões.

– 100 alunos acertaram a primeira questão.

– 99 alunos acertaram a segunda questão.

Quantos alunos erraram as duas questões?

1º questão = n(A)

2º questão = n(B)

Acertaram as duas questões → n(A ∩ B) = 50
Acertaram somente a questão A → n(A) – n(A ∩ B) = 100 – 50 = 50
Acertaram somente a questão B → n(B) – n(A ∩ B) = 99 – 50 = 49
Erraram as duas questões → U – n(A) – n(B) – n(A∩ B) = 200 – 50 – 50 – 49 = 51

Exercícios para resolvermos no curso

1) Uma editora estuda a possibilidade de lançar novamente as publicações Helena, Senhora e A Moreninha. Para isto, efetuou uma pesquisa de mercado e concluiu que em cada 1000 pessoas consultadas: 600 leram A Moreninha; 400 leram Helena; 300 leram Senhora; 200 leram A Moreninha e Helena; 150 leram A Moreninha e Senhora; 100 leram Senhora e Helena; 20 leram as três obras; Calcule:

a) O número de pessoas que leu apenas uma das obras.
b) O número de pessoas que não leu nenhuma das três obras.
c) O número de pessoas que leu duas ou mais obras.

Resposta:

O número de pessoas que leu apenas uma das obras é 270 + 120 + 70 = 460 :
O número de pessoas que não leu nenhuma das três obras é x = 1000 – 870 = 130 ;
O número de pessoas que leu duas ou mais obras é 180 + 20 + 130 + 80 = 410

2) (PUC) – Numa comunidade constituída de 1800 pessoas há três programas de TV favoritos: Esporte (E), novela (N) e Humanismo (H). A tabela abaixo indica quantas pessoas assistem a esses programas.2) (PUC) – Em uma empresa, 60% dos funcionários lêem a revista A, 80% lêem a revista B, e todo funcionário é leitor de pelo menos uma dessas revistas. O percentual de funcionários que lêem as duas revistas é ? .

Programas	E	N	H	E e N	E e H	N e H	E, N e H	Nenhum
Número de telespectadores	400	1220	1080	220	180	800	100	x

Através desses dados verifica-se que o número de pessoas da comunidade que não assistem a qualquer dos três programas é:

A) 200      B) os dados do problema estão incorretos       C) 900          D) 100        E) N.D.A

Resposta : Letra a