QUESTÃO 16. Duas torneiras enchem um certo tanque em três horas. Se a vazão de uma delas é a metade da vazão da segunda, em quantos minutos a torneira de menor vazão irá encher o mesmo tanque, se somente ela estiver aberta?
A) 270.
B) 900.
C) 360.
D) 540.
QUESTÃO 17. Em uma festa infantil, um mágico coloca em uma urna cinco bolas vermelhas, três brancas e duas azuis. Em seguida, escolhe um convidado e o desafia a retirar da urna duas bolas da mesma cor. Qual a probabilidade de o convidado ter sucesso na retirada das bolas?
A) 2/6075.
B) 23/50.
C) 14/45.
D) 3/1250.
E) 1/10.
QUESTÃO 18. Para comemorar seu aniversário, João convidou quatro amigos para jogar com ele um torneio de tênis. Considerando que, ao longo do torneio, cada participante jogará contra todos os outros jogadores uma única vez, quantas partidas serão realizadas?
A) 20.
B) 6.
C) 12.
D) 10.
E) 25.
QUESTÃO 19. Quando eu nasci, meu pai tinha dezenove anos e minha irmã um ano. Hoje a soma da minha idade com a de minha irmã supera a idade de meu pai em vinte e dois anos. Qual
a idade de minha irmã, em anos?
A) 40.
B) 4.
C) 41.
D) 5.
E) 20.
QUESTÃO 20. Em uma
turma da Escola Municipal Arco-Iris, os alunos foram entrevistados quanto aos esportes que praticavam. Entre as respostas foram citadas as seguintes modalidades: futebol, vôlei e basquete. Sabe-se que: 3 alunos não praticam nenhuma das três modalidades, 10 alunos praticam basquete; 15 jogam vôlei; 18 praticam futebol; 4 jogam futebol e basquete; 6 jogam basquete e vôlei; 8 jogam futebol e vôlei; e 2 praticam as três modalidades. Quantos alunos foram entrevistados?
A) 32.
B) 30.
C) 66.
D) 27.
E) 63.
QUESTÃO 21. João diz para Carlos a seguinte afirmação: Um número n inteiro positivo é primo quando só possui apenas dois divisores os quais são 1 e n. Baseado nessa afirmação
Carlos diz:
I – Todo número primo é ímpar.
II – O número 91 é primo.
III – A soma de dois números primos é sempre um número primo.
Ao analisar as afirmações de Carlos, a alternativa correta abaixo é:
A) I e II são verdadeiras e III é falsa
B) I e III são falsas e II é verdadeira
C) II e III são verdadeiras e I é falsa
D) I e II são falsas e III é verdadeira
E) I, II e III são falsas
QUESTÃO 22. Maria e Joana vão a uma sorveteria no shopping e ao chegar na sorveteria, Joana decide comprar 3 sorvetes onde é oferecido 6 sabores distintos. O número de maneiras que Joana pode escolher os sabores dos sorvetes é igual a:
A) 47
B) 56
C) 38
D) 29
E) 20
QUESTÃO 23 Arthur e Isaque brincam de desenhar retas r e s distintas e paralelas entre si. Arthur pede ao Isaque para marcar 5 pontos na reta r e 8 pontos na reta s e pergunta quantos triângulos podem ser formados com vértices nesses pontos. A figura abaixo mostra o modelo do desenho. Nessas condições o número de triângulos que Isaque formou foi:
A) 200 triângulos
B) 180 triângulos
C) 220 triângulos
D) 160 triângulos
E) 140 triângulos
QUESTÃO 24 O professor Cuca Legal brincando com seus alunos a respeito de números racionais e irracionais afirmou as seguintes sentenças: I – A soma de um número racional com um número irracional é igual a um número irracional. II – O produto de um número racional diferente de zero com um número irracional é igual a um número irracional. III – A soma de dois números irracionais é sempre igual a um número irracional. Baseado nas afirmações acima, a alternativa correta é:
A) I, II e III são verdadeiras
B) I e II são falsas e III é verdadeira
C) I e III são falsas e II é verdadeira
D) II e III são falsas e I é verdadeira
E) Apenas a III é falsa
QUESTÃO 25 Dois terrenos foram cercados em forma de triângulos como na figura abaixo.
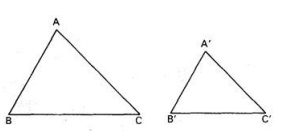
Sendo os terrenos triângulos semelhantes e que o Perímetro do terreno triangular A’B’C’ vale 30m e os lados do triângulo ABC são respectivamente 12m, 18m e 20m. O valor do menor lado do triângulo A’B’C’ é:
A) 7,8 m
B) 10,8 m
C) 9,2 m
D) 7,2 m
E) 6,8 m