Questão 1 até 3. Concurseiros e alunos do 5° Ano ao 9° Ano
Questão 4 até 7. Concurseiros
Questão 8 até 11. Do 5° Ano até 9° Ano
QUESTÃO 1. Assinale a alternativa que contém o algarismo que deveria ser o quinto da sequência numérica: 3, 6, 9, 12, . . .
A) 16
B) 13
C) 15
D) 18
E) 14
QUESTÃO 2. Assinale a alternativa que contém o algarismo que deveria ser o sexto da sequência numérica: 2, 7, 12, 17, 22, …
A) 26
B) 28
C) 30
D) 31
E) 27
QUESTÃO 3. Qual das alternativas contém o algarismo que deveria ser o quinto da sequência numérica: 52, 45, 38, 31, . . .?
A) 24
B) 26
C) 27
D) 25
E) 23
QUESTÃO 4. Nilton afirmou que, se o Brasil ganhasse a Copa, ele iria aprender a jogar futebol; Eraldo afirmou que, mesmo tentando, Nilton não aprenderia a jogar futebol; Marcos disse que só jogaria futebol, se o Brasil não ganhasse a Copa. Como o Brasil não ganhou a Copa, pode-se afirmar, sem possibilidade de erro, que
A) Eraldo falou a verdade.
B) Marcos foi jogar futebol.
C) Nilton não foi aprender a jogar futebol.
D) Marcos pode ter ido jogar futebol.
QUESTÃO 5. Suponha que você precise dividir 1 000 mililitros de uma determinada substância para a necropse de dois cadáveres, de forma diretamente proporcional às suas massas. Se um cadáver tem massa de 70 quilogramas e o outro tem massa de 55 quilogramas, a parte dessa substância, em mililitros, que caberá ao cadáver com maior massa será
(A) 560.
(B) 570.
(C) 550.
(D) 580.
(E) 540.
QUESTÃO 6. A figura representa uma foto, em formato retangular, que foi quadriculada de forma a resultarem 24 quadrados iguais cuja medida do lado, de cada um, é igual a 3 cm. Para ficar quadriculada com 4 vezes mais quadrados, iguais entre si, a mesma foto deve ser quadriculada de modo a serem obtidos quadrados iguais e com a medida do lado, em cm, igual a

(A) 1,5.
(B) 2.
(C) 1.
(D) 2,5.
(E) 3.
QUESTÃO 7. – Uma equipe de peritos criminais precisa descobrir a posição correta de um esconderijo e para tal dispõe somente do pedaço de um bilhete rasgado.

A equipe situa-se na posição desse poço que se encontra dentro de um terreno de área circular de raio igual a 100 passos e não possui bússola para indicar o norte. Além disso, é noite. O bilhete rasgado não deixa claro se o número de passos a ser dado é de múltiplos de três ou de oito. Entretanto, a equipe é formada por peritos que entendem de métodos de contagem e que decidem usar o princípio da inclusão-exclusão: “Sendo A e B conjuntos cujo número de elementos é dado por n(A) e n(B), respectivamente, então n(A U B) = n(A) + n(B) – n(A ∩ B), onde n(A U B) é o número de elementos que pertence a pelo menos um dos conjuntos A e B”. Com base nesse princípio, determine o número máximo de tentativas que a equipe terá de realizar para encontrar o esconderijo.
a) 33
b) 12
c) 45
d) 41
e) 4
QUESTÃO 8. Observe a reta numérica representada abaixo. Essa reta está dividida em segmentos de mesma medida.

O número correspondente ao ponto M é
A) 8,0
B) 8,5
C) 9,0
D) 9,5
QUESTÃO 9. Observe abaixo as dimensões internas de um reservatório de água, que possui formato de paralelepípedo retângulo
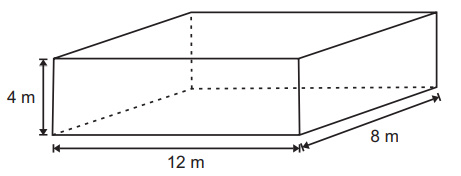
Qual é a quantidade máxima de água que esse reservatório suporta?
A) 24 m3
B) 56 m3
C) 100 m3
D) 384 m3
QUESTÃO 10. O resultado da expressão (– 3)2 + (– 45) ÷ 15 é
A) – 9
B) – 6
C) 6
D) 9
QUESTÃO 11. São necessários 4 baldes, totalmente cheios, para encher um reservatório de 30 litros. Quantos desses baldes, totalmente cheios, são necessários para encher um reservatório de 45 litros?
A) 6 baldes.
B) 7 baldes.
C) 8 baldes.
D) 9 baldes.