1. (INSTITUTO AOCP – 2016) No chute, qual é a probabilidade de alguém acertar duas questões em que só há as possibilidades “Verdadeiro” e “Falso”?
A) 0,15 B) 0,18 C) 0,20 D) 0,23 E) 0,25
Resolução – (Questão 1) – Probabilidade – Vídeo
2. (FGV – 2015) O quadro a seguir mostra a distribuição das idades dos funcionários de certa repartição pública:
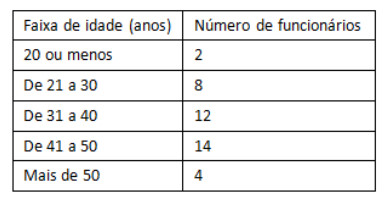
Escolhendo ao acaso um desses funcionários, a probabilidade de que ele tenha mais de 40 anos é:
A) 30%; B) 35%; C) 40%; D) 45%; E)55%.
3. (FGV – 2015 ) Uma urna contém apenas bolas brancas e bolas pretas. São vinte bolas ao todo e a probabilidade de uma bola retirada aleatoriamente da urna ser branca é 1/5. Duas bolas são retiradas da urna sucessivamente e sem reposição. A probabilidade de as duas bolas retiradas serem pretas é:
A) 16/25; B)16/19; C) 12/19; D) 4/5; E) 3/5;
Resolução – (Questão 3) – Probabilidade – Vídeo
4. (UPENET – 2014) Um dado não viciado é lançado 2 vezes. A probabilidade de aparecer o número 5 nos 2 lançamentos é de
A) 1/6 B) 1/66 C) 1/ 2 D) 1/36 E) 1/18
5. (UPENET – 2014) Jogamos duas vezes um dado não viciado. É CORRETO afirmar que a probabilidade de o produto dos números das faces superiores ser par é de
A) 1/6 B) 1/ 4 C) 3/ 4 D) 1/ 2 E) 0,38
6. (UPENET – 2014) O Departamento de Fiscalização de Trânsito dispõe de dez fiscais, sendo 5 do sexo masculino e 5 do sexo feminino. Pretende criar uma equipe com 3 fiscais sorteados ao acaso. Qual é a probabilidade de os componentes da equipe serem do mesmo sexo?
A) 1/6 B) 1/5 C) ¼ D) 1/3 E) ½
7. (UPENET) Em uma sala, esperam 6 (seis) homens e 4 (quatro) mulheres. São escolhidas, aleatoriamente, 3 (três) dessas pessoas. Nessas condições, sabendo que as três pessoas escolhidas são distintas, a probabilidade de haver, no máximo, uma mulher no grupo de pessoas escolhidas é igual a
A) 2/3 B) 1/3 C) ½ D) 1 E)3/ 4
8. (UPENET) . Considere um dado não viciado com seis faces distintas numeradas de 1 a 6. É CORRETO afirmar que
A) a probabilidade de a soma dos valores das faces obtidos em três lançamentos deste dado ser maior ou igual a 6 é de 100%.
B) a probabilidade de os valores das faces obtidos em dois lançamentos deste dado serem iguais é estritamente maior que a probabilidade de em algum destes dois lançamentos, o dado cair com face de valor par.
C) a probabilidade de a soma dos valores das faces obtidos em dois lançamentos deste dado ser igual a 5 é estritamente maior que à da mesma soma ser igual a 8.
D) probabilidade de a soma dos valores das faces obtidos em dois lançamentos deste dado ser igual a 8 é estritamente maior que a da mesma soma ser igual a 5.
E) a soma dos valores das faces obtidos em três lançamentos deste dado jamais pode ser igual a 6.
9. (COPEVE – ALGAS – 2014) Num experimento científico, é observado que apenas um dentre três eventos e1, e2 e e3 pode ser observado por vez. Sabendo-se que a probabilidade de ocorrer e1 ou e2 é de 55% e que a probabilidade de ocorrer e1 ou e3 é de 62%, qual a probabilidade de ocorrer e2 ou e3?
Resolução – (Questão 9) – Probabilidade – Vídeo
A) 17% B) 38% C) 45% D) 83% E) 91%
10. (COPEVE – ALGAS – 2014) Uma urna contém seis bolas de pesos e tamanhos iguais, duas delas identificadas pela letra S e as demais pelas letras A, C, E e O. Sorteando-se as bolas, uma a uma e sem reposição, qual é a probabilidade de que a ordem de retirada das bolas forme a palavra ACESSO?
A) 0,002 B) 0,008 C) 0,02 D) 0,032 E) 0,08
11. (COPEVE – CASAL – 2014) Truco é um jogo de cartas muito popular nas regiões sul e sudeste do Brasil. No jogo, utiliza-se o baralho tradicional, composto por quatro naipes de doze cartas. Pelas regras do jogo, um momento de sorte do jogador é quando ele possui três cartas de um mesmo naipe. Qual a probabilidade de que as três primeiras cartas distribuídas aos jogadores sejam do mesmo naipe?
A) 55/3243 B) 55/1081 C) 3/48 D) 3/16 E) 3/12
12. (COPEVE – ALGAS – 2014) Mensalmente, algumas amigas se reúnem para jantar em um restaurante badalado. Em cada ocasião, através do resultado de um jogo, uma delas é dispensada da conta. No mês passado, o jogo escolhido foi o lançamento de um dado: não pagaria a conta quem obtivesse o maior número de pontos, com realização de desempate, se mais de uma pessoa conseguisse esse maior número. Tendo deixado dinheiro e cartão de crédito na bolsa que ficou em casa, Gisele estava ansiosa para ser contemplada. Se era a última a lançar o dado, e a maior pontuação obtida anteriormente foi quatro pontos, qual era a probabilidade de Gisele livrar-se da despesa sem participar de desempates?
A) 6 B) 3 C) 1/2 D) 1/3 E) 1/6
13. (COPEVE – CASAL – 2014) Como sua filha mais velha nasceu em julho de 1986, o Sr. Fred havia escolhido 0, 7, 1, 9, 8, 6 para serem os seis dígitos da sua senha de acesso aos caixas eletrônicos de seu banco. Pensando em companhar as “normas” da Matemática (“zero à esquerda não tem valor”), ele escolheu um dos dígitos diferente de zero para ser o primeiro. Numa ocasião em que o Sr. Fred esqueça sua senha, qual a probabilidade de acertá-la na primeira tentativa?
A)1/720 B)1/600 C)1/120 D)1/72 E)1/60
14. (COPEVE – FEIRA GRANDE – 2014) Periodicamente, um cientista observou o resultado de um determinado experimento. Ele constatou que apenas dois eventos, e1 e e2, eram observáveis e que sempre apenas um deles era visto por vez. Outra constatação foi que a probabilidade de e1 ocorrer foi 25% da probabilidade de e2 ocorrer. Nessas condições, qual foi a probabilidade de e2 ocorrer?
Resolução – (Questão 14) – Probabilidade – Vídeo
A) 25% B) 50% C) 70% D) 75% E) 80%
15. (COPEVE – TRINCHEIRAS – 2014 – ADAPTADA) No lançamento de três dados, observou-se que os resultados são todos distintos. Qual é a probabilidade de que um desses resultados seja igual a 1?
A) 1/216 B) 3/54 C) 91/216 D) 1/10 E) 1/6
GABARITO: 1.E 2.D 3.C 4.D 5.C 6.A 7.A 8.A 9.D 10.A 11.B 12.D 13.B 14.E 15.C